物理世界中存在着各种各样由颗粒集合而成的堆积系统，而颗粒的形状、排列、相互作用等，对系统的物理特性有着决定性的影响。堆积问题的数学解，可以作为物理学中晶体结构的理论模型，广为人知的例子包括面心立方与密排六方这两种在三维无限空间中的等积球体最密堆积晶体结构。颗粒在受限空间中的最密堆积结构，由于跟材料研发、物流运输等多方面的工程问题相关，也因此引起了科学家的兴趣。其中，圆管中相等大小的硬球所形成的准一维柱状晶体结构，随着圆管与球体的直径比改变，展现出丰富多样的螺旋形结构 (见下图)，而这类结构可以作为纳米碳管中的C60富勒烯碳球、纳米通道中的共聚物、胶体晶体线、毛细管中的热响应微球、毛细管中的微气泡、流体驱动的聚合物自组装、圆管中的染色体状聚合物等多种实验系统的晶体模型。

与球形颗粒相比，形状呈各向异性的颗粒，相关的堆积问题研究较少。这类颗粒因为带有方向性，所以一般能形成更多类别的自组装结构，而颗粒的形状各向异性对相关的最密堆积排列产生什么影响，是一个有趣而重要的物理问题。我们通过蒙特卡洛模拟计算，把上述的圆管空间最密堆积问题延伸至相等大小的旋转椭球。通过改变圆管相对颗粒的尺寸比D和椭球的长短轴比A，他们在窄管的条件下发现了共3种螺旋形结构和4种非手性结构(见图1)，而这些结构都呈现出比较有趣的位置序和取向序。在螺旋形结构中，圆管曲面对堆积结构的影响较大，颗粒的方向因而呈旋转式的变化，颗粒的位置分布则类似于球体堆积的手性螺旋结构。而在非手性结构中，椭球受其形状各向异性影响较大，只出现少数特定的取向。对于相同的长短轴比，圆管边界的约束条件使扁椭球与长椭球出现不同的最密结构，打破了三维无限空间中椭球最密堆积的“扁椭球-长椭球”对称规律。

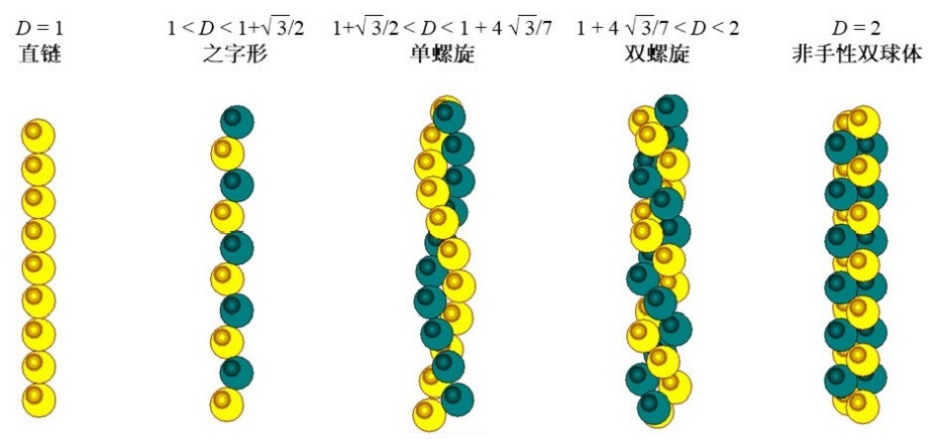
图 1 球体在窄圆管中的5种最密堆积晶体结构

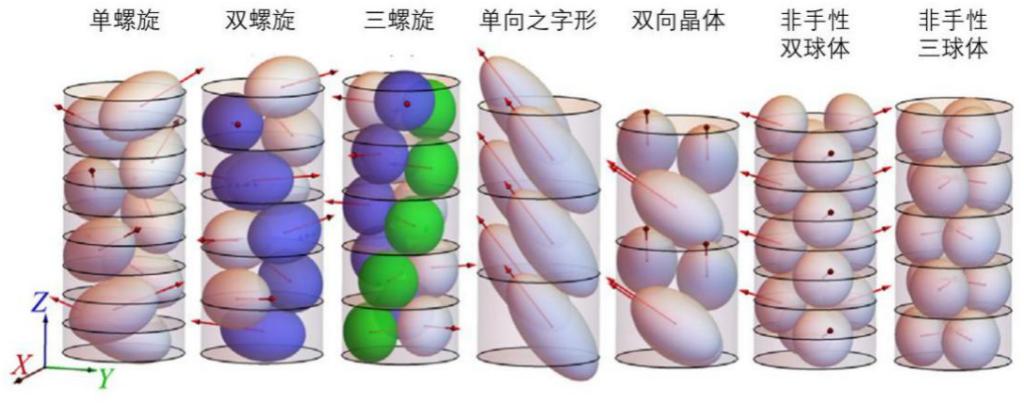
图 2 旋转椭球在窄圆管中的7种最密堆积晶体结构

    在窄管条件下，椭球颗粒已呈现了多达7种不同的最密堆积晶体结构，可见这只是冰山一角，还有更多的晶体结构有待发现。这项研究展示，我们可以通过改变D与A这两个几何参数，去调控系统在圆管边界约束条件所引发的手性序与形状各向异性所引发的方向序这两者之间的转变。研究成果可为新材料(例如由各向异性颗粒组成的胶体晶体线)的研发，提供理论基础。